OO第一单元总结
\(\mathcal{Author:gpf}\)
源码见 https://github.com/solor-wind/BUAA_OO
题目概述
第一单元的主题是表达式括号展开,要求读入一个包含加、减、乘、乘方以及括号的表达式,输出恒等变形展开所有必要括号括号后的表达式。
- 第一周:括号嵌套仅一层、单变量
- 第二周:新增表达式因子、自定义函数因子,允许多层嵌套
- 第三周:支持求导因子、函数定义时允许引用已定义函数。
量化分析
代码量
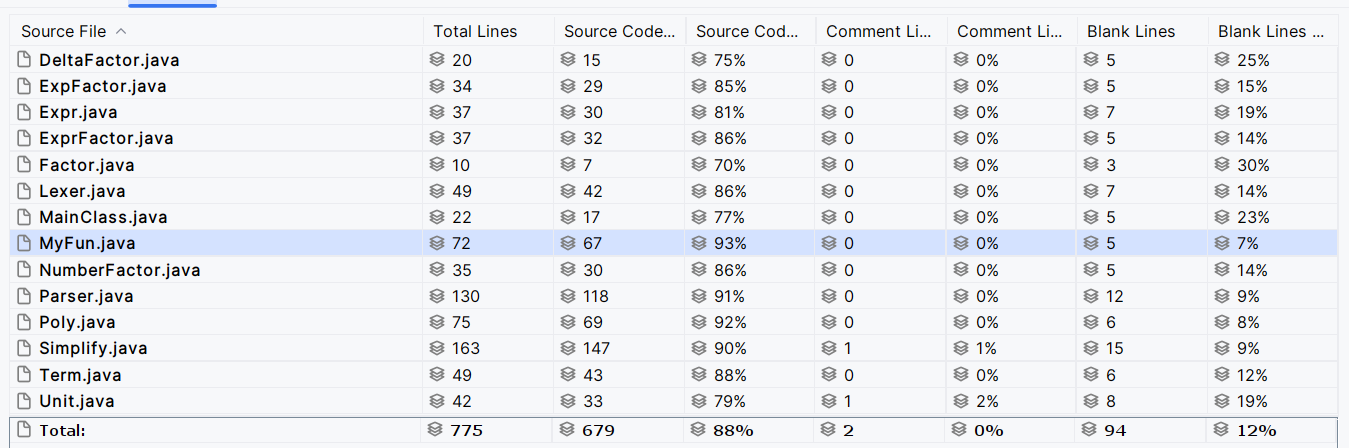
复杂度
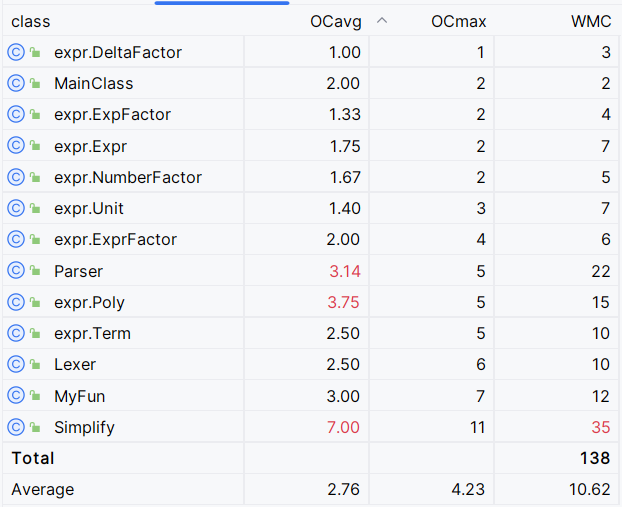
可以发现Simplify类的复杂度严重超标,主要原因是表达式化简需要对各种情况进行特判,而且还加入了提取最大公因数和对输入预处理的功能,导致复杂度过高
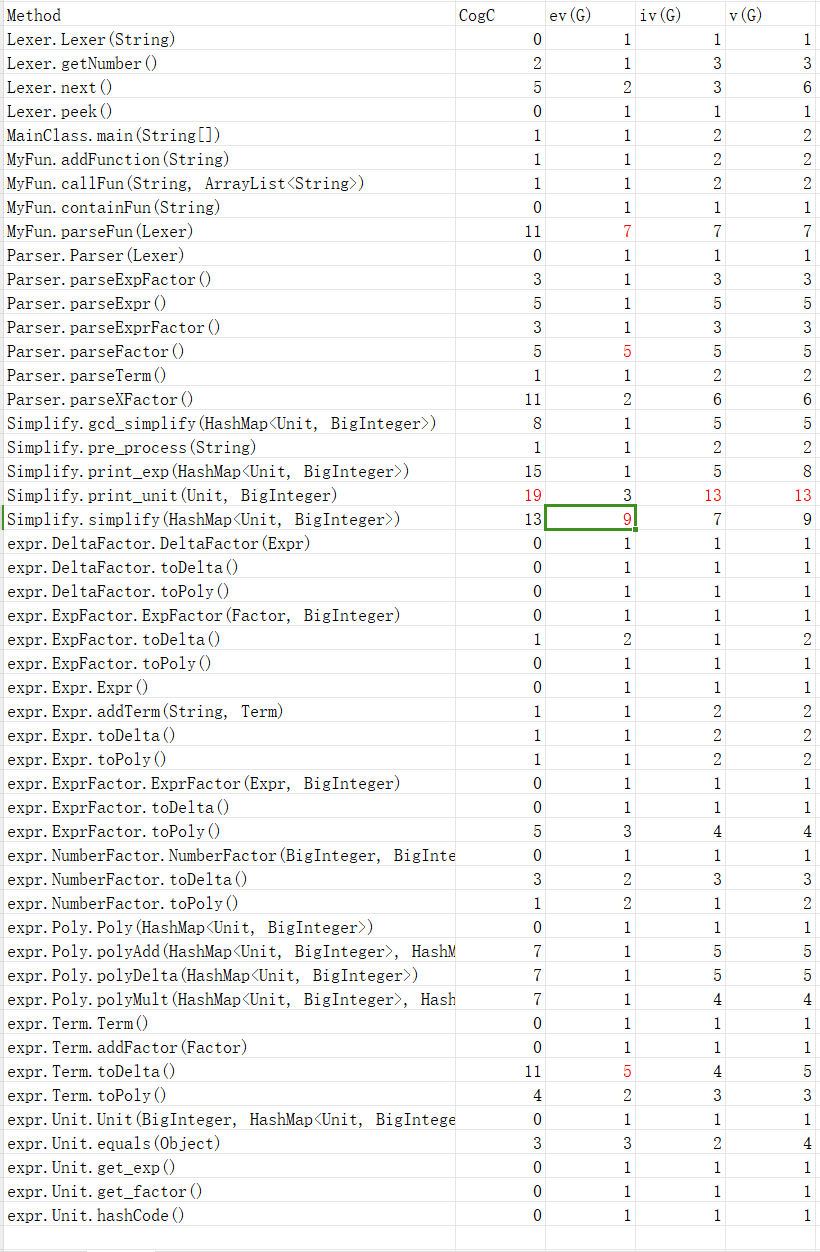
print_unit方法复杂度也严重超标,原因在于加入exp因子后,需要进行特判的情况增加,还要判断是否为表达式来化简括号,因此复杂度高。
思路与架构
先上类图
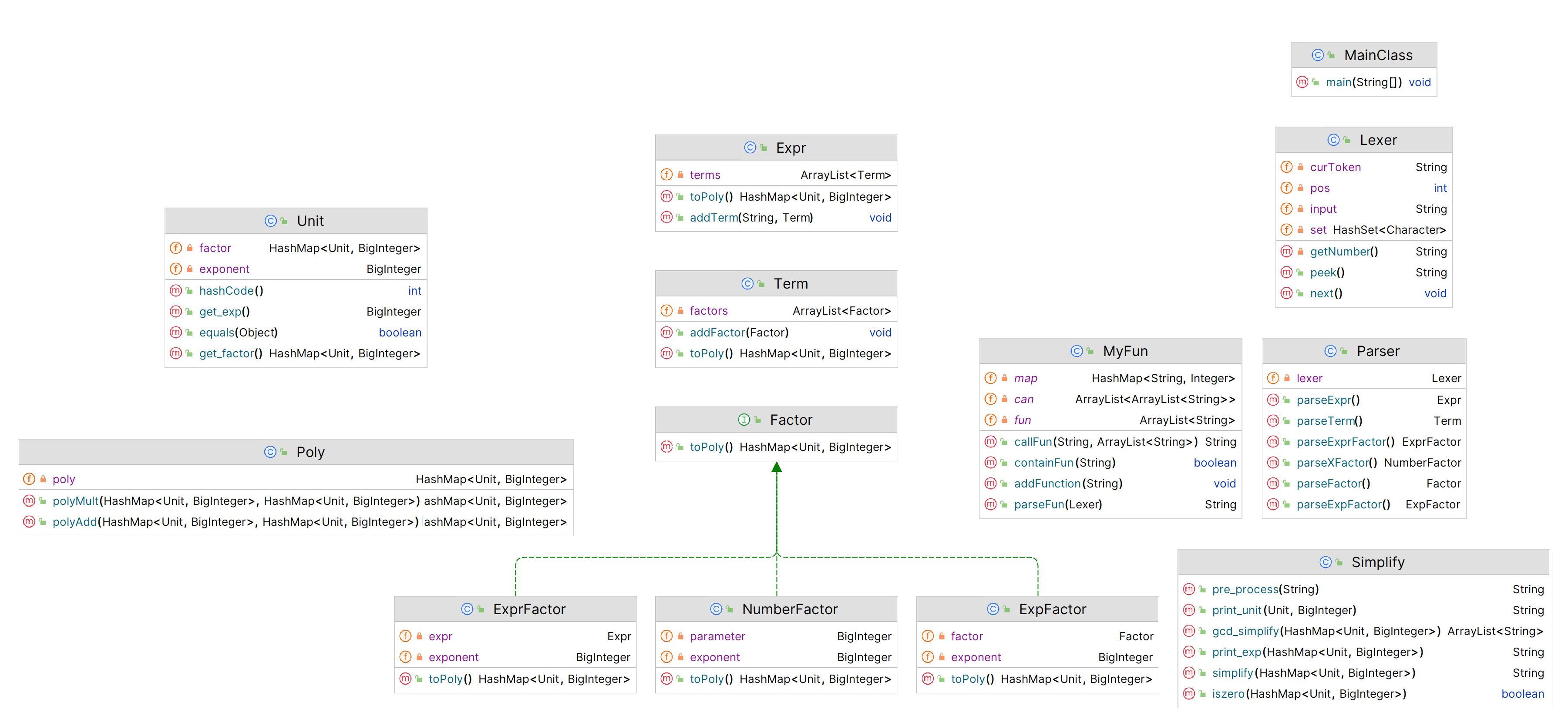
其中,程序的主体是先存储自定义函数,然后调用lexer对输入表达式进行词法分析,接着用parse进行输入解析,解析完毕后调用toPoly方法运算、转化成统一形式,最后进一步化简输出。
解析部分采用递归下降(有点编译原理的感觉),分为表达式、项、因子三个层次。表达式解析调用项的解析方法,项再调用因子的解析方法,如果是表达式因子等特殊因子还可以再调用表达式解析方法直至解析完毕。主要因子均继承Factor接口,方便统一管理,内部属性与特点相对应。解析自定义函数调用时采用字符串递归替换的方法,具体实现在myFun类中。
计算方面采用标准项统一处理,建立Unit类作为HashMap的key,相同即可合并。表达式类、项类、每种因子类均实现了toPoly方法转化为
HashMap<Unit,BigInteger>
类型,便于运算、化简、输出。多项式加法、乘法、求导写成了静态方法放进Poly类中。类似的,预处理与化简方法也写成了静态方法放进Simplify类中。
输入预处理
这一部分较为简单,直接用正则表达式对字符串进行匹配替换即可,主要是去掉空白符和连续的正负号方便后续处理。
1 | |
替换完毕后,将自定义函数的函数名、指定的形参、函数体分别存放。
1 | |
输入解析
首先使用lexer(词法分析器),逐个读入字符并分类为数字、变量、+-等符号,提供peek(返回当前的token,即遇到了什么)、next(读入下一个token)方法。
parser采用递归下降的方法,将表达式拆解为表达式、项、因子三层:
- 表达式遇到加减号调用解析项的方法,将解析完的内容加到项容器中(容器中的元素是加减关系)
- 项遇到乘号调用解析因子的方法,将解析完的内容加到因子容器中(容器中的元素是相乘关系)。
- 解析因子的方法根据当前Token的不同,调用不同的解析方法
1 | |
自定义函数的解析
关于自定义函数因子,我并没有相应的因子类,而是通过字符串递归替换得到没有自定义函数的字符串,然后调用lexer、parser等方法去解析,再返回结果
1 | |
表达式的存储
上面已经介绍过表达式、项的存储方法,现在介绍各类因子的存储
常量、幂函数因子
常量和幂函数可以统一成 \(a\times x^b\) 的形式
1 | |
表达式因子
内部用一个表达式类存储即可,再加上表达式括号后面的指数
1 | |
指数函数因子
由于指数函数内部也是一个因子,因此用Factor来存储。虽然有种无限递归的感觉,但暂时没有出问题。同样还要存储后面跟的指数
1 | |
求导因子
事实上极其简单,甚至最初我还将它直接归类到表达式因子。但事实上求导因子的toPoly方法要调用表达式类的toDelta方法,自身的toDelta方法要先调用表达式类的toDelta方法,再求导一次。而表达式因子只有toDelta方法会求导,且仅求一次导数。
1 | |
表达式计算
核心思想有两个,第一个还是递归调用,第二个是存算分离。
总体结构1——递归调用
这里的递归调用类似解析部分的递归下降法。
- 表达式依次调用存储的项的
toPoly方法,获得结果后进行多项式加法并返回 - 项依次调用存储的因子的
toPoly方法,获得结果后进行多项式乘法并返回 - 因子实现
toPoly方法,如果内部存储有表达式,直接调用表达式的toPoly方法再处理即可
求导方法类似,但需要用到以下几个公式 \[ \begin{aligned} (a\times x^b\times e^c)'&=a\times b\times x^{b-1}\times e^c+a\times x^b\times e^c\times(c)'\\ [f(g(x))]'&=f'(g(x))g'(x)\\ (\prod_i f_i)'&=\sum_if_i'(\prod_{j\neq i}f_j)\\ \sum f_i&=\sum f_i' \end{aligned} \] 大体结构如上,但如何进行合并化简呢?
总体结构2——存算分离
存储时只存储相应因子的必要部分,计算时再化为统一的Unit或Poly类进行处理。
考察所有类别的因子,可以发现都能化成形如 \(a\times x^b\times \exp(c)\)
的基本项。因此,我决定采用Unit类来表示,并在存储的各类中添加toPoly方法转化成
HashMap<Unit,BigInteger> poly
来计算,Unit存储b和c,相同即可合并
注意以自建类作key时,一定要在类中重写equals和HashCode方法!
1 | |
- 系数a:Unit类中不存储系数,而是由各个因子中的toPoly方法将系数填写到
HashMap中的value中 - 指数b:存储在Unit的
BigInteger exponent中 - 指数函数中的嵌套因子c:转化成多项式后,存储在Unit的
HashMap<Unit,BigInteger> factor中
例如,2可以在计算过程中转化成多项式
HashMap<Unit,BigInteger> poly
,poly的大小为1,包含一个键值对,key为Unit,value为2。由于3为常数,所以Unit中指数项exponent为0,存储指数函数因子的factor为空。
又如,\(3\times x^6\times
\exp(1+x^2)\) 可以转化成多项式
HashMap<Unit,BigInteger> poly
,poly的大小为1,包含一个键值对,key为Unit,value为3。Unit里又存储了指数6和因子
\(x^2+1\) ,其中因子为
HashMap<Unit,BigInteger> factor
。factor的大小为2,有2个键值对,其中key1是Unit1,value1为1(代表1);key2是Unit2,value2为1(代表
\(x^2\)
)。Unit1中exponent为0,用factor为空代表 \(\exp(0)\)
;Unit2中exponent为2,factor同样为空。
在IDEA中可以看到如下的展开式
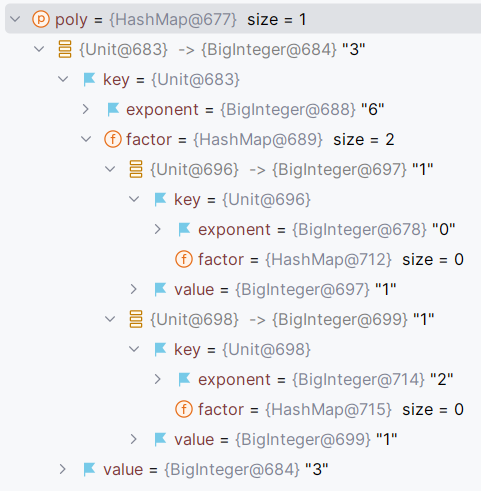
根据如上的思路,我们可以在表达式类、项类和所有因子类中构建toPoly方法将表达式转化为统一形式
性能优化与拓展性
注意到在第二次作业中,有部分测试点进行了边界压力测试,如果采用的方法不当,极有可能出现MLE或TLE的情况,比如测试点
1 | |
关于MLE:在处理表达式因子或指数函数因子后的指数时,如果采用向相应容器(比如项类的容器)中存入指数个因子的方法,那么在应对上述情况时很有可能爆内存,而且计算时会进行递归调用,产生很多重复计算。
关于TLE:在计算表达式时,如果采用展开所有项(如 \((x+1)^2=x^2+x+x+1\) )的方法而不合并,则在应对较大数据时计算效率会大大下降,建议边计算边合并。
目前架构能做到 (x+1)^1000
秒算,新增因子时,只需新建因子类、完善Unit类中的属性、修改Poly类中的加减法、添加输出方式即可,总体架构仍然可以保持不变
结果化简
由于题面允许指数函数后接指数,即允许 exp(2)^10
存在,于是可以用 \(\exp(a*x+b*y)=\exp(x)^a+\exp(y)^b\)
这一公式进行任意优化。
但是,注意到以下几个例子:
exp((10000+10000*x))=exp((1+x))^10000exp((2*x))=exp(x)^2exp((10+20*x+20*x^2))=exp((2+4*x+4*x^2))^5exp((1+3*x))^2=exp((2+6*x))exp((3*x+2*x^2+2*x^3+2*x^4+2*x^5))=exp(x)*exp((x+x^2+x^3+x^4+x^5))^2
这说明无法单纯的提出来最大公因数来得到最优解,因为无法确定提出什么因数合适、是否要将因数合并进去 。所以,我选择正确性优先,在保证正确性的基础上,寻找最大公因数并提取,并与最初的表达式的长短比较得出相对较短的字符串并输出。
评测机与bug
和好友ZX共同完成了评测机。
数据生成
框架
采用python编写,具体框架即课程组给定的形式化表述。
- 首先主函数调用生成自定义函数的函数(可选),然后根据指定的样例数调用表达式生成函数
- 表达式生成函数根据一定的概率调用一定数量的项生成函数,拼接成表达式
- 项生成函数根据一定的概率调用一定数量、一定种类的因子生成函数,拼接成项
- 常数、自变量因子直接返回,表达式因子、求导函数因子会递归调用表达式生成函数,指数函数因子会一定概率调用表达式生成函数
具体的一些细节如空白符、正负号、前导0、指数的产生封装成小函数。
功能
基本实现了所有类型样例的全覆盖,但缺点就是随机程度高,需要大量样例才能全覆盖。生成各种因子以及许多参数均可个性化调整,存储在json文件中,目前支持的参数主要有:测试样例数、是否自动生成自定义函数(或者自己指定函数)、括号嵌套层数上限、表达式中项数量的上限、项中因子数量的上限、产生各种因子的概率、空白符等多余内容的概率……
正确性判定
主要方法有两种——对拍与syms库
对拍采用讨论区JZY大佬的方法即可,两人分别跑一次数据,再用其中一个人跑一下刚才二人的结果的相减,若最终结果为0,则可以认为大概率没有问题
syms库即python中的库,这部分的实现主要由好友ZX完成,大致包括表达式结果的预处理(如dx替换为diff)、调用数据生成器和java并运行、结果比较与输出、超时跳过(Linux可选)。
bugs
很幸运第一单元的作业没有在强测、互测中发现bug,以下测试点均为互测中有效hack数据,主要通过评测机发现。
1.0
1 | |
2.0
1 | |
3.0
1 | |
心声
开学第一天即王炸
相比上学期的OOpre,这周的作业可谓是疾如猛火。开学第一天即布置高强度作业,最终码量甚至逼近OOpre的总码量,而且思维难度更高,对架构、性能要求也更高。
第一周幸好有训练单元提供的架构,输入解析改一改即可,直接省了近一半的代码量。但剩下的部分任然不可小觑,借鉴了学长的博客后还是采用了自己的架构,简单省事,用
HashMap<BigInteger,BigInteger>
存储多项式,也为第二周的重构埋雷。
第二周比第一周更难,主要是指数函数因子的出现让我不得不思考如何存储才能在计算时快速合并。反复阅读学长博客后,我不得不承认学长的架构自有其道理,但其中的细节还需要自己思考、处理,比如以Unit作key。最终重构后的代码也在强测中取得了良好的表现,看来以后决不能偷偷省事,一定要预先思考需求、做好架构。
第三周由于第二周的良好架构,作业发布当晚就写完了,最终码量775/679(总行/非空行)。
总的来说,OO不失为一次涅槃,高强度的码量与高难度的作业迫使我们一次又一次的思考架构。第一单元的作业让我对递归下降的解析法理解更加深刻,同时对层次化设计的思想也有了一定的应用经验。