离散3笔记
\(\mathcal{Author:gpf}\)
第二章 排列与组合
计数原理
加法原理:
乘法原理
减法原理:\(|A|=|U|-|\bar{A}|\)
除法原理
排列
与顺序有关的摆放/选择,默认线性排列
集合的一个排列即以某种顺序列出集合的所有元素(全排列)
排列数 \(P(n,k)=\dfrac{n!}{(n-k)!}=nP(n-1,k-1)=P(n-1,k)+kP(n-1,k-1)\) 相当于n个元素选k个全排列,集合的k排列(有k个元素的排列)
循环排列:除法原理,每种循环排列对应n种线性排列,即 \((n-1)!\)
项链题目下,翻转后相同,即对应2n种线性排列
例外:n男n女相间坐在圆桌旁,则先排男,后排女,共 \((n-1)!n!\) 种方法
组合
与顺序无关的摆放/选择
组合数 \(\dbinom{n}{k}=\dfrac{n!}{k!(n-k)!}\) 表示n个集合元素的k子集(有k个元素的子集)
帕斯卡公式:\(\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)
多重集
多重集的排列
允许元素重复的特殊“集合”,如 \(M=\{a,a,b,b,b\}\) ,可写作 \(M=\{2\cdot a,3\cdot b\}\) ,其中2 3称M的重数
无限重复数,k种不同元素,则S的r排列个数为 \(k^r\)
有限重复数全排列:设S是多重集,k种不同元素,每种重复数为 \(n_1\cdot a_1,n_2\cdot a_2,...,n_3\cdot a_3\) ,则所有元素的排列种数为 \(\dfrac{n!}{n_1!\cdot n_2!...n_k!}\)
也可解释为将n个元素的集合划分成k个有标签的盒子 \(B_1,B_2,...B_k\) ,其中 \(B_i\) 含有 \(n_i\) 个元素,则划分方法数为 \(\dfrac{n!}{n_1!\cdot n_2!...n_k!}\) 。盒子无标号且 \(n_1=n_2=..=n_k\) 则 \(\dfrac{n!}{k!\cdot n_1!\cdot n_2!...n_k!}\)
例题,车的排列
多重集的组合
多重集S的一个r组合是S的一个子多重集,可表示为方程 \(x_1+x_2+...+x_k=r\) 的非负整数解的个数,其中 \(0\leqslant x_i\leqslant\min(n_i,r)\) ,或多重集 \(T=\{r\cdot 1,(k-1)\cdot *\}\) 的r排列数
无限重复数下,r组合方法数为 \(\dbinom{r+k-1}{r}\) (k个元素)
证明:设有k=4个数字,每个数字可用无数次,问r=5组合是多少
以 \(\{2,3,3,3,4\}\) 为例,将其按大小顺序排好后 \(\{2,3,3,3,4\}\Leftrightarrow\{2+0,3+1,3+2,3+3,4+4\}=\{2,4,5,6,8\}\)
类似的,\(\{\infty\cdot1,\infty\cdot2,\infty\cdot3,\infty\cdot4\}\) 的5组合等价于 \(\{1,2,...,8\}\) 的5组合,从而得证
例题:取自 \(1,2,...k\) 的长为r的非递减序列个数为 \(\dbinom{r+k-1}{r}\)
例题2:从 \(1,2,...n\) 中取出 \(r\) 个不相邻的数的方法有 \(\dbinom{n-r+1}{r}\) ,可视为将取出的r个数插入剩下的n-r个数中
技巧:灵活转化集合计数与方程解的个数问题,后者可用变量代换转化成新的问题。当有上界约束时,可枚举有上界的变量
| n个元素 | r排列 | r组合 |
|---|---|---|
| 无重复 | \(P(n,r)\) | \(\dbinom{n}{r}\) |
| 无限重复 | \(n^r\) | \(\dbinom{n+r-1}{r}\) |
| 有限重复 | \(\dfrac{n!}{n_1!\cdot n_2!...n_k!}\) (全排列) | 容斥原理 |
鸽巢原理
简单形式
定义:如果把 \(n+1\) 个物体放进 \(n\) 个盒子,那么至少有一个盒子包含两个或更多的物体
划分类问题
如果有n+1个整数,且整数小于等于2n,是否一定会有一对数互质?
答:存在。划分成n组相邻的数,必有相差1的一组数被同时取出。
前缀和、整除类
求证:在m个数正整数 \(a_1,a_2,...,a_m\) 中,存在 \(0\leqslant k<l<m\) ,使得 \(a_{k+1}+a_{k+2}+...+a_{l}\) 能够被m整除
答:考虑前缀和,共m个,总有一个被m整除、或者除m的余数相同
连续时间类
某厂在五年期间的每一个月里至少试制一种新产品,每年最多试制19种新产品,试证明:一定存在连续几个月,恰好试制24种新产品

中国剩余定理
设\(m,n\) 是互质的正整数, \(a\) 和 \(b\) 分别是小于 \(m\) 和 \(n\) 的非负整数,则存在正整数 \(x\) ,满足 \(x\equiv a\pmod{m},x\equiv b\pmod{n}\)

加强形式
定义:令 \(q_1,q_2,...,q_n\) 为正整数,如果将 \(q_1+q_2+...+q_n-n+1\) 个物体放进 \(n\) 个盒子里,则:
- 或者第1个盒子里至少含有 \(q_1\) 个物体,
- 或者第2个盒子里至少含有 \(q_2\) 个物体,
- 或者第 \(n\) 个盒子里至少含有 \(q_n\) 个物体。
推论:设 \(n\) 和 \(r\) 都是正整数,若 \(n(r-1)+1\) 个物体放入 \(n\) 个盒子,则至少有一个盒子含有至少 \(r\) 个物体
例题1:
证明:从任意给出的5个正整数中必能选出3个数,它们的和能被3整除。
答:任意正整数除以3的余数只能为0,1或2。设A为任意给出的5个正整数的集合。设 \(t_0,t_1,t_2\) 为A中除以3余数分别为0,1,2的数的个数。
若 \(t_0,t_1,t_2\) 均不为0, 则一定有三个数除以3的余数分别 为0,1,2,则这三个数的和能被3整除。
若 \(t_0,t_1,t_2\) 中至少有一个为0,不妨设 \(t_0=0\) 则 \(t_1+t_2=5\)
由平均原理知,至少有 \(\lceil5/2\rceil=3\) 个数除以3的余数相同(全为1或全为2),则这三个数的和能被3整除
例题1.5:转盘问题,见PPT
例题2:
证明由 \(n^2+1\) 个实数构成的序列 \(a_1,a_2,...,a_{n^2+1}\) 或者含有长度为n+1的递增子序列,或者含有长度为n+1的递减子序列
答:假设不存在长度为n+1的递增子序列,只需构造长度为n+1的递减子序列。
设 \(l_k\) 是以 \(a_k\) 为起始的最长递增子序列长度,\(k=1,2,...n^2+1\) ,则对 \(\forall k\) 有 \(1\leqslant l_k\leqslant n\) 。对序列 \(l_1,l_2,...,l_{n^2+1}\) ,一定存在 \(\lceil(n^2+1)/n\rceil=n+1\) 个 \(l_i\) 相等,设 \(l_{k_1}=l_{k_2}=...=l_{k_{n+1}}\) ,其中 \(1\leqslant k_1<k_2<...<k_{n+1}\leqslant n^2+1\) ,下证 \(a_{k_1},a_{k_2},...,a_{k_{n+1}}\) 是长度为n+1的递减序列
如果存在 \(k_i,k_{i+1}\) ,使得 \(a_{k_i}<a_{k_{i+1}}\) ,则可以把 \(a_{k_i}\) 加到以 \(a_{k_{i+1}}\) 开始的最长递增子序列的开头,则有 \(l_{k_i}>l_{k_{i+1}}\) ,矛盾。因此 \(a_{k_1},a_{k_2},...,a_{k_{n+1}}\) 为递减序列
Ramsey定理
简单形式:6个人中或者有3个人彼此认识,或者有三个人彼此互不认识
定理:如果 \(m\geqslant2,n\geqslant2\) ,则一定存在正整数 \(p\) 使得 \(K_p\rightarrow K_m,K_n\) 。(当把 \(K_p\) (有p个节点的完全图)的边着成红色或蓝色时,或者存在一个红色 \(K_m\) ,或者存在一个蓝色 \(K_n\) )
定义:Ramsey数是使得 \(K_p\rightarrow K_m,K_n\) 成立的最小整数p,记为 \(r(m,n)\)
- \(r(m,n)=r(n,m)\)
- \(r(2,n)=n,r(m,2)=m\)
- \(r(m,n)\leqslant r(m-1,n)+r(m,n-1),m,n\geqslant3\)
推广形式:多个颜色,即 \(K_p\rightarrow K_{n_1},K_{n_2},...,K_{n_l}\) ,此时Ramsey数形式为 \(r(n_1,n_2,...,n_l)\)
生成排列和组合
排列生成算法
递归生成
邻位对换
对任一给定的正整数k,加上一个箭头使之成为 \(\overrightarrow{k}\) 或 \(\overleftarrow{k}\) 。如果整数k的箭头指向与其相邻但比它小的整数,则称k是可移动的。
初始状态:\(\overleftarrow{1}\overleftarrow{2}...\overleftarrow{n}\)
若还存在活动整数,则
- 求出最大的活动整数 \(m\)
- 交换m和其箭头指向的相邻整数的位置
- 改变所有满足 \(p>m\) 的整数 \(p\) 的箭头方向
不存在活动整数时,算法结束
排列的逆序
定义:设 \(i_1,i_2,...,i_n\) 是集合 \(\{1,2,...,n\}\) 的一个排列,如果 \(0\leqslant k<l\leqslant n\) ,且 \(i_k>i_l\) ,称数对 \((i_k.i_l)\) 是排列的一个逆序。记 \(a_j\) 是排列中先于整数 \(j\) 并大于 \(j\) 的个数,用于度量 \(j\) 的反序程度,称为 \(j\) 的逆序数,同时称排列 \(a_1,a_2,...,a_n\) 为排列 \(i_1,i_2,...,i_n\) 的逆序列
排列和其逆序列一一对应,从逆序列求排列只需从最大数/最小数开始排即可
逆序个数为奇数称奇排列,反之称偶排列
组合生成算法
n元集合 \(S=\{x_0,x_1,...,x_{n-1}\}\) 的所有组合与长度为n的二进制数一一对应
n阶Gray反射码:
- 1阶反射码是0,1
- 设 \(n>1\)
且n-1阶反射Gray码已经构造,则n阶反射Gray码如下
- 以n-1阶的顺序列出,将0添加到开头
- 再反序将n-1列出,将1添加到开头
逐次法生成Gray码:
- 初始 \(a_{n-1}...a_1a_0=0...00\)
- 当 \(a_{n-1}...a_1a_0\ne10...0\)
时,进行以下操作:
- 计算 \(\sigma(a_{n-1}...a_1a_0)=a_{n-1}+...+a_1+a_0\)
- 如果 \(\sigma(a_{n-1}...a_1a_0)\) 是偶数,则改变 \(a_0\) ,否则确定j,使得 \(a_j=1\) 且对于所有 \(i<j,a_i=0\) ,改变 \(a_{j+1}\)
设 \(a_{n-1},...,a_1,a_0\) ,定义 \(b_i=\begin{cases}0,\sum\limits_i^{n-1}a_j是偶数\\1,\sum\limits_i^{n-1}a_j是奇数\end{cases}\) ,则 \(a_{n-1}...a_1a_0\) 在Gray码序表的位置是 \(b_{n-1}\times2^{n-1}+...+b_1\times2+b_0\)
生成r子集
子集的“先于”和“后继”:子集内部从小到大排列后,按字典序来。如 \(\{1,2,3\}\) 先于 \(\{2,3,4\}\)
\(\{1,2,...,n\}\) 的字典序r子集的生成算法:从12..r开始,逐个列出直接后继直至得到(n-r+1)(n-r+2)...n
二项式系数
二项式
帕斯卡公式:\(\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)
二项式定理:\((x+y)^n=\sum\limits_{k=0}^n\dbinom{n}{k}x^{n-k}y^k\)
例:证明 \(\sum\limits_{k=0}^n\dbinom{n}{k}^2=\dbinom{2n}{n},n\geqslant0\)
答:右侧为从2n个集合中选n个元素,等号左侧即从2个n组元素中总共取n个元素的方法数
证明方法:帕斯卡公式、求导积分、组合证明
链
链:设S是n个元素的集合,S上的一条链是S的子集的集合C,其中对于C中的每一对子集,总有一个包含在另一个之中
最大链:n个元素的集合S,S上最大链 \(C=\{A_0,A_1,...,A_n\}\) 满足 \(A_0=\phi\subset A_1...\subset A_n\) ,且 \(|A_i|=i(i=1,...,n)\) 。最大链的构造与排列类似,数目为 \(n!\)
反链:即没有子集包含在另一子集中
构造反链的方法之一:取集合S的所有k子集的集合。S上的一条反链最多包含 \(\dbinom{n}{\lfloor n/2\rfloor}\) 个子集
链其实相当于有限偏序集的可比关系,反链即不可比
令 \((X,\leqslant)\) 是一个有限偏序集,令r是最大链的大小,则X可以被划分成r个反链,但不能被划分为少于r个反链
令 \((X,\leqslant)\) 是一个有限偏序集,令m是最大反链的大小,则X可以被划分成m个链,但不能被划分为少于m个链
对称链划分:设 \(S=\{1,2,...,n\}\) ,如果S的幂集 \(\mathcal{P}(S)\) 的一个链划分满足
- 链中每一个子集比它前面的子集的元素个数多1
- 链中第一个子集与最后一个子集的大小和等于n
如 \(S=\{1,2,3\}\) ,\(C_1:\phi\subset\{1\}\subset\{1,2\}\subset\{1,2,3\}\) ,\(C_2:\{2\}\subset\{2,3\}\) ,\(C_3:\{3\}\subset\{1,3\}\)
构造方法:

多项式定理
\((x_1+x_2+...+x_t)^n=\sum\limits_{n_1+n_2+...+n_t=n}\dbinom{n}{n_1n_2...n_t}x_1^{n_1}x_2^{n_2}...x_t^{n_t}\)
其中 \(\dbinom{n}{n_1n_2...n_t}=\dfrac{n!}{n_1!n_2!...n_t!}\) 为多项式系数
多项式的帕斯卡公式:\(\dbinom{n}{n_1n_2...n_t}=\dbinom{n-1}{(n_1-1)n_2...n_t}+\dbinom{n-1}{n_1(n_2-1)...n_t}+...\dbinom{n-1}{n_1n_2...(n_t-1)}\)
牛顿二项式定理
令 \(\alpha\) 是一个实数,对于所有满足 \(0\leqslant|x|<|y|\) 的变量x,y,有 \((x+y)^{\alpha}=\sum\limits_{k=0}^{\infty}\dbinom{\alpha}{k}x^ky^{\alpha-k}\) ,其中 \(\dbinom{\alpha}{k}=\dfrac{\alpha(\alpha-1)...(\alpha-k+1)}{k!}\)
应用:\((1+z)^{\alpha}=\sum\limits_{k=0}^{\infty}\dbinom{\alpha}{k}z^k\) ( \(|z|<1\) )
容斥原理
集合S不具有性质 \(P_1,P_2,...,P_m\) 的元素的个数为 \(|\overline{A_1}\cap...\cap\overline{A_m}|=|S|-\sum|A_i|+\sum|A_i\cap A_j|-\sum|A_i\cap A_j\cap A_k|+...+(-1)^m|A_1\cap A_2\cap...\cap A_m|\)
集合S至少具有性质 \(P_1,P_2,...,P_m\) 之一的元素的个数为 \(|A_1\cup...\cup A_m|=\sum|A_i|-\sum|A_i\cap A_j|+\sum|A_i\cap A_j\cap A_k|+...+(-1)^{m+1}|A_1\cap A_2\cap...\cap A_m|\)
一道有坑点的例题:求1-1000中不能被5、6、8整除的数
设 \(A_1,A_2,A_3\) 分别为能被5、6、8整除的数的集合,则 \(|A_2\cap A_3|=\lfloor1000/24\rfloor\ne\lfloor1000/(6*8)\rfloor\)
最终答案为600
在多重集组合的应用
例1:确定多重集 \(T=\{3·a,4·b,5·c\}\) 的10子集的个数 解: 令多重集 \(T^*=\{∞·a,∞·b,∞·g\}\) 的所有10子集的集合为 S, \(A_1\) 是S中包含多于 3个a 的10子集的集合, \(A_2\) 是S中包含多于 4个6 的10子集的集合, \(A_3\) 是S中包含多于 5个c的10子集的集合, 那么,T的10-组合数等于 \(|\bar{A_1}\cap \bar{A_2}\cap \bar{A_3}|\)
错位排列
\(D_n=n!(1-\dfrac{1}{1!}+\dfrac{1}{2!}-\dfrac{1}{3!}+...+(-1)^n\dfrac{1}{n!})\)
\(D_n=(n-1)(D_{n-1}+D_{n-2})=nD_{n-1}+(-1)^n\)
禁止位置的排列:令 \(X_1,X_2,...,X_n\) 是 \(\{1,2,...,n\}\) 的子集,用 \(P(X_1,X_2,...,X_n)\) 表示 \(\{1,2,...,n\}\) 的排列 \(i_1i_2...i_n\) 的集合,使得 \(i_1\notin X_1,i_2\notin X_2,...,且i_n\notin X_n\) 。记 \(p(X_1,X_2,...,X_n)=|P(X_1,X_2,...,X_n)|\) 表示 \(P(X_1,X_2,...,X_n)\) 中排列的个数
即对于P中的任意排列,位置i不能出现集合 \(X_i\) 中的元素
解决方法:容斥原理
应用:带禁止位置的“非攻击车”

相对禁止问题
旋转木马
\(Q_n=D_n+D_{n-1}\)
生成函数与递推关系
常用展开式
\[ e^x=\sum\limits_{n=0}^\infty\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+...+\dfrac{x^n}{n!}+...\\ e^{-x}=\sum\limits_{n=0}^\infty(-1)^n\dfrac{x^n}{n!}=1-x+\dfrac{x^2}{2!}+...+(-1)^n\dfrac{x^n}{n!}+...\\ \dfrac{1}{2}(e^x+e^{-x})=1+\dfrac{x^2}{2!}+\dfrac{4^2}{4!}+...+\dfrac{x^{2n}}{2n!}+...\\ \dfrac{1}{2}(e^x-e^{-x})=x+\dfrac{x^3}{3!}+\dfrac{5^2}{5!}+...+\dfrac{x^{2n+1}}{(2n+1)!}+... \]
生成函数
令 \(h_0,h_1,...,h_n,...\) 为一无穷数列,其生成函数 \(g(x)\) 定义为 \(g(x)=h_0+h_1 x+...+h_n x^n+...\)
与多重集组合的关系
设 \(h_n\) 是多重集 \(S=\{\infty\cdot a_1,\infty\cdot a_2\,...,\infty\cdot a_k\}\) 的n组合的个数,求数列 \(h_0,h_1,...,h_n\) 的生成函数 \(g(x)\)
因 \(h_n=\dbinom{n+k-1}{n}\) ,所以 \(g(x)=\sum\limits_{n=0}^\infty\dbinom{n+k-1}{n}x^n=\dfrac{1}{(1-x)^k}(|x|<1)\) \[ \begin{aligned} g(x)&=\dfrac{1}{(1-x)^k}=\dfrac{1}{1-x}\times\dfrac{1}{1-x}\times...\times\dfrac{1}{1-x}\\ &=(\sum\limits_{e_1=0}^\infty x^e_1)(\sum\limits_{e_2=0}^\infty x^e_2)...(\sum\limits_{e_k=0}^\infty x^e_k)\\ &=(1+x+...+x^{e_1}+...)(1+x+...+x^{e_2}+...)...(1+x+...+x^{e_k}+...)\\ &=\sum\limits_{e_1+...+e_k=n=0}^\infty x^{e_1}x^{e_2}...x^{e_k} \end{aligned} \] 其中,项 \(x^n=x^{e_1}x^{e_2}...x^{e_k}\) 满足 \(e_1+e_2+...+e_k=n\) ,因此项 \(x^n\) 的系数 \(h_n\) 是方程 \(e_1+e_2+...+e_k=n\) 的非负整数解的个数,也即n组合的个数

与排列逆序数的关系
设 \(h(n,t)\) 表示 \(\{1,2,...,n\}\) 的排列中有t个逆序的排列的数目,则数列 \(h(n,0),h(n,1),...,h(n,n(n-1)/2)\) 的生成函数为 \(g(x)=1(1+x)...(1+x+...+x^{n-1})\)
证明:展开 \(g(x)\) 后,每一项形如 \(x^{a_1}x^{a_2}...x^{a_n}\) ,且 \(0\leqslant a_i\leqslant i-1\) ,与排列中每个元素的逆序数一一对应,且和为逆序数。
指数生成函数
\(g^{(e)}(x)=h_0+h_1 x+h_2\dfrac{x^2}{2!}+...+h_n\dfrac{x^n}{n!}+...\)
与多重集排列的关系
设n是正整数, \(P(n,k)=\dfrac{n!}{(n-k)!}\) 表示n元素集合的k排列的数目,则数列 \(P(n,0),P(n,1),...,P(n,n)\) 的指数生成函数为 \[ \begin{aligned} g^{(e)}(x)&=P(n,0)+P(n,1)x+P(n,2)\dfrac{x^2}{2!}...+P(n,n)\dfrac{x^n}{n!}\\ &=1+nx+\dfrac{n!}{2!(n-2)!}x^2+...+\dfrac{n!}{k!(n-k)!}x^k+...+\dfrac{n!}{n!0!}x^n\\ &=(1+x)^n \end{aligned} \] 数列 \(1,1,1,...,1,...\) 的指数生成函数为 \(g^{(e)}(x)=\sum\limits_{n=0}^\infty\dfrac{x^n}{n!}=e^x\)
设多重集 \(S=\{n_1\cdot a_1,n_2\cdot a_2,...,n_k\cdot a_k\}\) ,设 \(h_n\) 是S的n排列数,则数列 \(h_1,h_2,...,h_k,...\) 的指数生成函数为 \(g^{(e)}(x)=f_{n_1}(x)f_{n_2}(x)...f_{n_k}(x)\) ,其中 \(f_{n_i}(x)=1+x+\dfrac{x^2}{2!}+...+\dfrac{x^{n_i}}{n_i!}\)
对 \(a_i\) 的约束将反映到 \(f_{n_i}(x)\) 上

递推关系
设数列为 \(h_0,h_1,h_2,...h_n,..\) ,若存在量 \(a_1,a_2,..,a_k(a_k\ne0)\) 和量 \(b_n\) (每个量是常数或依赖于n的数)使得 \(h_n=a_1h_{n-1}+a_2h_{n-2}+...+a_{k-1}h_{n-k+1}+a_kh_{n-k}+b_n\) ,则称该数列满足k阶线性递推关系。若 \(b_n=0\) ,则称该数列是k阶线性齐次递推关系。若 \(a_i\) 均为常数,则称该数列是k阶常系数线性递推关系
常系数线性齐次递推关系
对于 \(h_n=a_1h_{n-1}+a_2h_{n-2}+...+a_kh_{n-k}(a_k\ne0,n\geqslant k)\)
特征方程法:
- 解方程 \(x^k-a_1x^{k-1}-...-a_{k-1}x-a_k=0\) ,得到方程的根
- 若根 \(q_i\) 不重复(不是重根),则对应于 \(q_i\) 的部分为 \(H_n^{(i)}=c_iq_i^n\)
- 若根 \(q_i\) 是 \(s_i\) 重根,则对应于 \(q_i\) 的部分为 \(H_n^{(i)}=(c_1+c_2n+...+c_{s_i}n^{s_i-1})q_i^n\)
- 递推关系的通解即为 \(h_n=H_n^{(1)}+H_n^{(2)}+...+H_n^{(t)}\)
- 最终带入k个初始值求解常数 \(c_i\) 即可
生成函数法:

常系数线性非齐次递推关系
\(h_n=a_1h_{n-1}+a_2h_{n-2}+...+a_kh_{n-k}+b_n(a_k\ne0,b_n\geqslant0,n\geqslant k)\)
求解步骤:
- 求齐次的通解
- 求非齐次的特解
- 组合通解和特解,并利用初始项求常系数c
类似常系数线性非齐次微分方程的求法
尝试特解时,可根据 \(b_n\) 特征来试探
- 若 \(b_n\) 是n的k次多项式,则尝试 \(h_n\) 也是n的k次多项式
- 若 \(b_n\) 是指数形式,则尝试 \(h_n\) 也是指数形式
注意:若通解的指数和特解的指数相同,则特解应设为 \(d^n*(多项式)\) ,多项式最高次项的次数为重数。(类比微分方程的特解求法)
特殊计数序列
Catalan数
Catalan数列为 \(C_0,C_1,...,C_n,...\) ,其中 \(C_n=\dfrac{1}{n+1}\dbinom{2n}{n},n=0,1,2,...\) 是第n个Catalan数。其几何意义是凸n+1边形被在其内部不相交的对角线划分成三角形区域的方法数 \(h_n=C_{n-1}\) 。
满足递推式 \(C_n=C_0C_{n-1}+C_1C_{n-2}+...+C_{n-1}C_0\)
具体应用:
- 括号化问题。对于n个矩阵连乘,有多少种方法加括号。\(h_n=C_{n-1}\)
- 出栈次序问题。一个栈的进栈序列为 \(1,2,...,n\) ,则有 \(C_n\) 种出栈序列
- 二叉树问题。共n个节点,则 \(C_n\) 种
考虑n个+1和n个-1构成的2n项序列 \(a_1,a_2,...,a_{2n}\) ,其部分和总满足 \(a_1+a_2+...+a_k\geqslant0(k=12,...,2n)\) 的序列的个数等于第n个Catalan数
设 \(p\) 和 \(q\) 是正整数且 \(p\geqslant q\) ,则从 \((0,0)\) 到 \((p,q)\) 且不穿过 \(y=x\) 的方法数为 \(\dfrac{p-q+1}{p+1}\dbinom{p+q}{q}\)
差分序列和Stirling数
差分
0阶差分序列:\(h_0,h_1,h_2,...,h_n,...\)
1阶差分序列:\(\Delta^1h_n=h_{n+1}-h_n\)
k阶差分序列:\(\Delta^kh_n=\Delta(\Delta^{k-1}h_n)=\Delta^{k-1}h_{n+1}-\Delta^{k-1}h_n\)
类似微分、求导,其实就是整数化了(
差分表
其中,第0行元素为 \(1,6,15,28,...\)
第0条对角线为 \(1,5,4,0,0,...\)
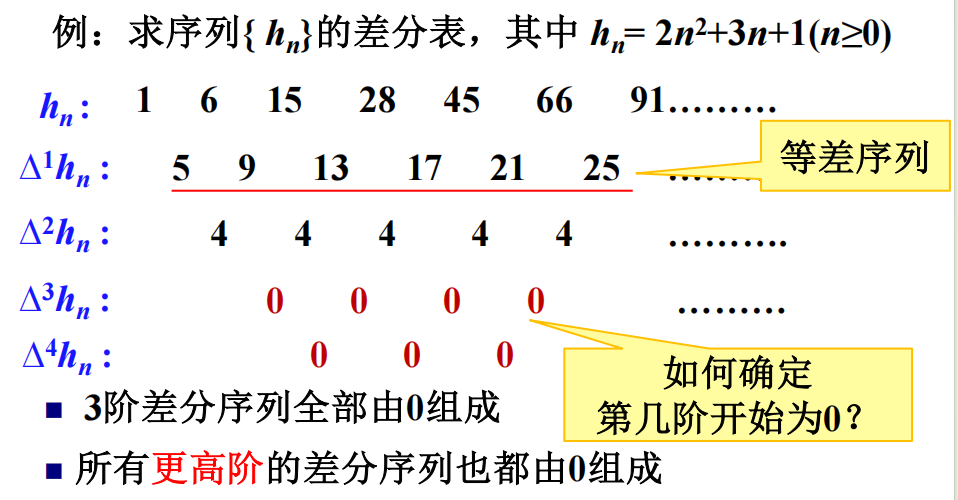
若差分表的第0条对角线为 \(c_0,c_1,...,c_p,0,0,...(c_p\ne0)\) ,则数列的通项满足
\(h_n=c_0\dbinom{n}{0}+c_1\dbinom{n}{1}+...+c_p\dbinom{n}{p}\)
\(\sum\limits_{k=0}^nh_k=c_0\dbinom{n+1}{1}+c_1\dbinom{n+1}{2}+...+c_p\dbinom{n+1}{p+1}\)
设数列 \(h_n=n^p\) 的第0条对角线的第k个元素为 \(c(p,k)\) ,则有 \(c(p,0)=\begin{cases}1,p=0\\ 0,p\geqslant1\end{cases}\) ,以及 \(c(p,p)=p!\) ,上式也可化为
\(h_n=n^p=c(p,0)\dbinom{n}{0}+c(p,1)\dbinom{n}{1}+...+c(p,p)\dbinom{n}{p}\)
第二类stirling数
设 \([n]_k=P(n,k)\) 是从n个元素中取k个元素的排列数,由于 \(\dbinom{n}{k}=\dfrac{n(n-1)...(b-k+1)}{k!}=\dfrac{[n]_k}{k!}\) ,从而 \(h_n=\sum\limits_{k=0}^p\dfrac{c(p,k)}{k!}[n]_k\)
令 \(S(p,k)=\dfrac{c(p,k)}{k!}(0\leqslant k\leqslant p)\) 称为第二类Stirling数,组合意义是把p个元素划分到k个不可区分的盒子且没有空盒的划分的个数
\(S(p,0)=c(p,0),S(p,p)=1\) ,且满足递推公式 \(S(p,k)=kS(p-1,k)+S(p-1,k-1),(1\leqslant k\leqslant p-1)\)
类比组合数的公式
当盒子有区别时,\(S^\#(p,k)=k!S(p,k)\)
对每一个满足 \(0\leqslant k\leqslant p\) 的整数k,有 \(S^\#(p,k)=\sum\limits_{t=0}^k(-1)^t\dbinom{k}{t}(k-t)^p\) ,从而 \(S(p,k)=\dfrac{S^\#(p,k)}{k!}\)
用容斥原理证明
Bell数为将p个元素划分到不可区分的盒子且没有空盒的划分个数(对盒子数量无要求,相当于分成几堆),\(B_p=S(p,0)+S(p,1)+...+S(p,p)\)
Bell数满足递推式 \(B_p=\dbinom{p-1}{0}B_0+\dbinom{p-1}{1}B_1+...+\dbinom{p-1}{p-1}B_{p-1}\)
第一类Stirling数 :将p个物品排成k个非空的循环排列的方法,记为 \(s(p,k)\)
\([n]_p=n(n-1)...(n-(p-1))=a_n^pn^p-a_n^{p-1}n^{p-1}+...+(-1)^{p-1}a_n^1n^1+(-1)^pa_n^0n^0\)
其中 \(a_n^k=s(p,k)\) ,且有 \(s(p,0)=0(p\geqslant1),s(p,p)=1(p\geqslant0)\)
满足递推式 \(s(p,k)=(p-1)s(p-1,k)+s(p-1,k-1)\)
总结
| p个球,k个盒 | 是否为空 | 方案数 |
|---|---|---|
| 盒有区别 | \(k^p\) | |
| 盒无区别 | \(\sum\limits_{i=1}^{\min(p,k)}S(p,i)\) | |
| 盒有区别 | 无空盒 | \(k!S(p,k)\) |
| 盒无区别 | 无空盒 | \(S(p,k)\) |
| k个循环排列 | 非空 | \(s(p,k)\) |
\(S(p,k)=\dfrac{1}{k!}\sum\limits_{t=0}^k(-1)^t\dbinom{k}{t}(k-t)^p\)
\(S(p,k)=kS(p-1,k)+S(p-1,k-1),(1\leqslant k\leqslant p-1)\)
\(s(p,k)=(p-1)s(p-1,k)+s(p-1,k-1)\)
分拆数
设一个正整数n,若存在正整数集 \(\{n_1,n_2,...,n_k\}(1\leqslant k\leqslant n,1\leqslant n_i\leqslant n)\) ,使得 \(n_1+n_2+...+n_k=n\) ,则称这个正整数集是n的一个分拆,称每个 \(n_i\) 为n的一个部分。记n的所有包含k个部分的不同分拆的个数为 \(p_n^k\) ,n的所有不同分拆的个数为 \(p_n\) ,成为n的分拆数
设 \(a_1,a_2,...,a_n\) 是n个非负整数,且 \(n=na_n,(n-1)a_{n-1}+...+2a_2+a_1\) ,则上式对应n的一个分拆记作 \(\lambda=n^{a_n}...2^{a_2}1^{a_1}\) 。n的分拆数的个数也等价于上面方程的非负整数解的个数
分拆数满足递推关系 \(\sum\limits_{j=1}^kp_n^j=p_{n+k}^k\)
设 \(p_n(r)\) 是最大部分为r的n的分拆的个数,\(q_n(r)\) 是满足分拆各部分不大于r的n-r的分拆数量,则 \(p_n(r)=q_n(r)\)
分拆数定理:正整数n分成k个部分的分拆个数,等于n分成以k为最大部分的分拆个数
分拆图

看成矩阵,其转置被称为共轭分拆,记为 \(\lambda^*\) 。分拆与共轭分拆完全相同则称为自共轭分拆
n的自共轭分拆个数等于n分拆成互不相同的若干奇数的和的分拆个数
把n分成奇数部分的分拆个数等于把n分成不同部分的分拆个数
分拆数数列 \(p_0,p_1,...,p_n,...\) 的生成函数为 \(g(x)=\sum\limits_{n=0}^\infty p_nx^n=\prod\limits_{k=1}^\infty(1-x^k)^{-1}\) ,证明如下:



着色计数
置换群与对称群
给定集合G和G上的二元运算 \(\cdot\) ,若以下四个条件满足,则称代数结构 \((G,\cdot)\) 为群:
- 封闭性:运算在G上封闭,即对于任意 \(a,b\in G\) ,都有 \(a\cdot b\in G\)
- 结合律:\(a\cdot(b\cdot c)=(a\cdot b)\cdot c\)
- 存在单位元:存在 \(e\in G\) ,对于任意 \(a\in G\) ,满足 \(e\cdot a=a\cdot e=a\) ,\(e\) 称为G的单位元
- 存在逆元:对任意 \(a\in G\) ,存在 \(a^{-1}\in G\) ,满足 \(a\cdot a^{-1}=a^{-1}\cdot a=e\)
例如 \(G=\{-1,1\}\) 在乘法运算下是一个群,整数集Z在加法运算下是一个群
有限群:G有限。此时 \(|G|\) 称为群的阶
循环群:若存在 \(a\in G\) ,G中任意元素b均可以表示成a的幂,则该群为循环群,a为生成元
置换:设X是一个有限集,X的每个置换可视为X到自身的双射,即 \(X=\{1,2,...,n\}\) 的置换可表示为 \(\begin{pmatrix}1&2&...&n\\i_1&i_2&...&i_n\end{pmatrix}\) ,个数为 \(n!\) 。记X的所有置换所组成的集合为 \(S_n\)
置换的合成:设f和g为 \(\{1,2,...,n\}\) 上的两个置换 \[ f=\begin{pmatrix}1&2&...&n\\i_1&i_2&...&i_n\end{pmatrix}\ ,g=\begin{pmatrix}1&2&...&n\\j_1&j_2&...&j_n\end{pmatrix} \] 则f与g按照先f后g的顺序放置得到一个新运算 \[ g\circ f=\begin{pmatrix}1&2&...&n\\j_1&j_2&...&j_n\end{pmatrix}\circ\begin{pmatrix}1&2&...&n\\i_1&i_2&...&i_n\end{pmatrix} \] 其中 \((g\circ f)(k)=g(f(k))=j_{i_k}\)
置换的合成实质上定义了 \(S_n\) 上的一个二元运算,满足结合律但不满足交换律 。恒等置换、逆置换类似恒等函数、逆函数
置换群:若 \(S_n\) 的非空子集G满足群的要求,则称G是X的一个置换的群,简称置换群。
置换群满足消去律,\(X=\{1,2,...,n\}\) 的所有置换的集合 \(S_n\) 以及置换的合成是一个置换群,称为n阶对称群


着色
设集合 \(X=\{1,2,...,n\}\) ,以及X的置换群 \(G\) ,则X的一种着色方案c是对X的每一个元素指定一种颜色的方案,令 \(c\) 表示X的一种着色,\(c(i)\) 表示 \(i\) 的颜色
令C表示X中所有着色的集合,令 \(f=\begin{pmatrix}1&2&...&k&...&n\\i_1&i_2&...&i_k&...&i_n\end{pmatrix}\) 是G中的一个置换,定义 \(f*c\) 是使 \(i_k\) 具有颜色 \(c(k)\) 的着色,即 \((f*c)(i_k)=c(k)\)
f将k变到 \(i_k\) ,k的颜色 \(c(k)\) 移到 \(f(k)=i_k\) 并成为 \(i_k\) 的颜色。
点不动,颜色动
着色集C需要满足:对G中的任意置换f和C中的任意着色c,\(f*c\) 任然属于C
\((g\circ f)*c=g*(f*c)\)
着色等价关系:X,G,C,\(f*c\in C\) 。设 \(c_1\) 与 \(c_2\) 是C中的任意两种着色,若存在G中的一个置换 \(f\) ,使得 \(f*c_1=c_2\) ,则称两种着色等价,记为 \(c_1\sim c_2\)
Burnside定理
计算X的非等价着色数的公式
稳定核:使着色c保持不变的G中所有置换的集合 \(G(c)=\{f|f\in G,f*c=c\},c\in C\)
推论:
- 任何着色c的稳定核也能形成一个置换群
- 对G中任意置换f与g,\(g*c=f*c\) 当且仅当 \(f^{-1}\circ g\in G(c)\)
引理:与c等价的着色数 \(|\{f*c|f\in G\}|\) 等于G的置换个数除以c的稳定核中的置换个数,即 \(|\{f*c|f\in G\}|=\dfrac{|G|}{|G(c)|}\)
Burnside定理:设G是X的置换群,C是X中满足“对G中的任意置换f和C中的任意着色c,\(f*c\) 任然属于C”的着色集合,则C中非等价的着色数 \(N(G,C)=\dfrac{1}{|G|}\sum_{f\in G}|C(f)|\) 。其中 \(C(f)=\{c|c\in C,f*c=c\}\)
即在G中的置换作用下保持不变的着色的平均数
计算步骤:
- 确定置换群G
- 确定着色集C
- 计数G中每个置换f的不变着色集 \(C(f)\) 的大小
- 使用Burnside公式
Polya计数
循环置换:如果在一个置换中,某些元素以循环的方式置换且余下元素保持不变,则称这样的置换为循环置换,简称循环

循环因子分解:设f是集合X的任意置换,\(D_f=(X,A_f)\) 是顶点集为X且边集为 \(A_f=\{(i,f(i)|i\in X\}\) 的有向图, \[ [i_1\ i_2\ ...\ i_p],[j_1\ j_2\ ...\ j_q],...,[l_1\ l_2\ ...\ l_r] \] 为 \(D_f\) 所对应的有向圈,则f可以分解为: \[ f=[i_1\ i_2\ ...\ i_p]\circ[j_1\ j_2\ ...\ j_q]\circ...\circ[l_1\ l_2\ ...\ l_r] \] 称为f的循环因子分解
记置换f的循环分解中的循环个数为 \(\#(f)\) ,则用k中颜色对X进行着色,f保持C中着色不变的着色数为 \(|C(f)|=k^{\#(f)}\)
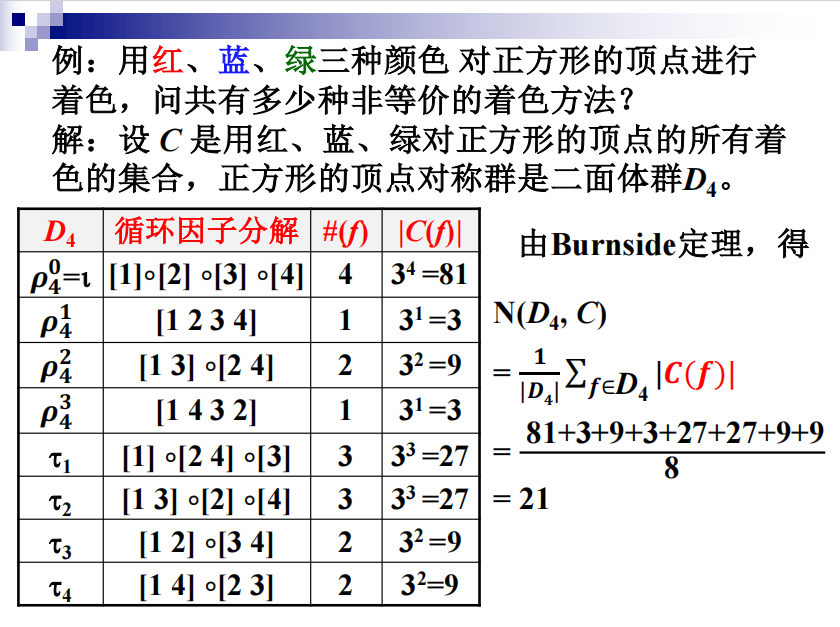
限制条件下的着色
设f的循环因子分解中有 \(e_i\) 个i循环,则 \(1e_1+2e_2+...+ne_n=n\) ,记 \(type(f)=(e_1,e_2,...,e_n)\) 为置换f的类型。循环数为 \(\#(f)=e_1+e_2+...+e_n\)
定义置换f的单项式为 \(mon(f)=z_1^{e_1}z_2^{e_2}...z_n^{e_n}\) ,G中的置换按照类型的生成函数是G中所有置换的单项式的和,即 \(\sum_{f\in G}mon(f)\) 。G的循环指数定义为生成函数除以置换个数,即 \(P_G(z_1,z_2,...,z_n)=\dfrac{1}{|G|}\sum_{f\in G}z_1^{e_1}z_2^{e_2}...z_n^{e_n}\)
设集合 \(X=\{1,2,...,n\}\) ,用k种颜色对X进行着色,C是X的所有 \(k^n\) 种着色的集合,G是X的置换群,则非等价的着色数是用 \(z_i=k\) 带入G的循环指数得到的数,即 \(N(G,C)=P_G(k,k,...,k)\)
有限制时的情况如下所示:

应用:图的同构
考前公式
\(P(n,k)=P(n-1,k)+kP(n-1,k-1)\)
\(\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}\)
令 \(\alpha\) 是一个实数,对于所有满足 \(0\leqslant|x|<|y|\) 的变量x,y,有 \((x+y)^{\alpha}=\sum\limits_{k=0}^{\infty}\dbinom{\alpha}{k}x^ky^{\alpha-k}\) ,其中 \(\dbinom{\alpha}{k}=\dfrac{\alpha(\alpha-1)...(\alpha-k+1)}{k!}\)
多重集组合 \(g(x)=\sum\limits_{n=0}^\infty\dbinom{n+k-1}{n}x^n=\dfrac{1}{(1-x)^k}(|x|<1)\)